Rowe, D.B. (2003). Multivariate Bayesian Statistics: Models for Source Separation and Signal Unmixing. CRC Press, Boca Raton, FL, USA. ISBN: 1584883189. List price $124.95. Available from CRC Press, Amazon.com, or BN.com.

The Reverend

Thomas Bayes

Bayesian Source Separation

There are many problems in many disciplines such as acoustics, EEG, MEG, fMRI, Radar, and Surveillance which can be cast as the source separation problem (SS). Any signal that is believed to be made up of a linear combination of elementary signals is a SS problem. The real world source separation problem is more difficult than it appears at first glance. 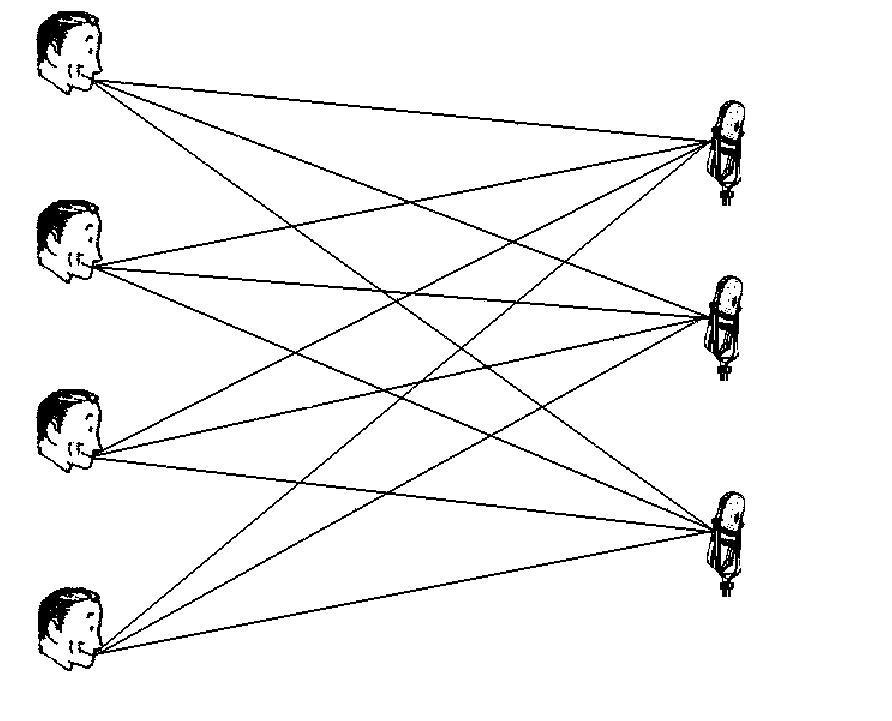First the problem is described assuming that the mixing process is instantaneous and constant over time. A Bayesian statistical solution is then described. These assumptions are subsequently alleviated with a model and a likelihood describing correlated source components and vectors with changing delays. A Bayesian statistical solution is described. If you would like to skip over my specific work and continue with only the description of the BSS problem, then skip the sections with asteriks.


Source Separation
Bayesian Source Separation
Translated to Portuguese


Source Separation
The
following is based on Multivariate Bayesian Statistics: Models for Source Separation and Signal Unmixing by Rowe. The problem addressed by source separation is that of separating unobservable or latent source signals when mixed signals are observed. In other words, to take a set of observed mixed signal vectors and unmix or separate them into a set of true unobservable source signal vectors.

Introduction

Cocktail Party

To
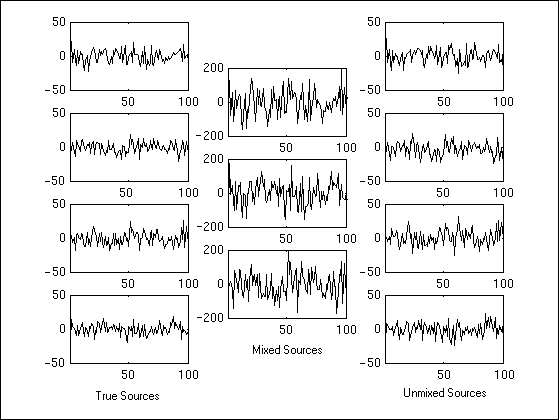
motivate the separation of sources model, consider context of the classic "Cocktail Party" problem. At a cocktail party, there are p microphones that record or observe m partygoers or speakers at n time increments. The observed conversations consist of mixtures of true conversations. The problem is to unmix or recover the original conversations from the recorded mixed conversations. A given microphone Calrad 500c Microphone is not placed to a given speakers mouth and is not shielded from the other speakers. Party
Each microphone records a mixture of all of the speakers.

Mixing Process


In
other words, we will be recording (observing) p-dimensional mixed signal vectors xi=(xi1,...,xip)' and the goal is to separate or unmix these observed signal vectors into the m-dimensional (component) true underlying source signal vectors, si=(si1,...,sim)' where i = 1,...,n are the time increments. The figure below visually shows the idea with the true speakers conversations in the first column, the microphones observed conversations in the middle column, and the unmixed speakers conversations in the last column. Note that there are m=4 speakers and p=3 microphones. We observe the middle column (the microphone recordings) and want the first column (the original conversations). From the recordings we obtain estimates of the original conversations (the last column). This is the unmixing process.

True, Mixed, and Unmixed Signals


Various
approaches with variations have been employed to try and solve the real world cocktail party problem. The most popular seems to be independent components analysis (ICA). Unfortunately, ICA has little promise at solving the cocktail party problem. At a cocktail party, the speakers are usually broken up into in small conversation groups. See the picture of a cocktail party above. Within each of these groups, the partygoers are not speaking independently. The partygoers are speaking in an obviously correlated fashion. One person is usuall speaking at a given time in a group. The independence assumption in ICA phohibits this obvious fact. ICA assumes that each person is babbeling without regard to the other people. That is, ICA models the case where we go into a room, press play on m tape recorders and record on p microphones. The Bayesian approach of Rowe seems to be the most promising at solving the real cocktail problem. It allows for dependent speakers.

The
general separation of sources model is

(xi|si,m) = f(si|m) + εi ,
(p x 1) (p x 1) (p x 1)

where f(si|m) is a function that mixes the source signals and εi is the measurement error. Using a Taylor series expansion, the function f, with appropriate assumptions can be expanded about the vector c and written as

f(si|m) = f(c) + f'(c)(si - c) + · · ·

and taking the first two terms, approximated by

f(si|m) = f(c) + f'(c) (si - c)
f'(si|m) = [f(c) - f'(c) c] + f'(c) si
f(si|m) = µ + Λ si

where f '(c) and Λ are p x m matrices. This is the linear synthesis model. More formally the adopted model is

(xi|µ,Λ,si,m) = µ + Λ si + ε i ,
(p x 1) (p x 1) (p x m) (m x 1) (p x 1)

where
µ = a p-dimensional unobserved population mean vector, µ = (µ1,...,µp)';
Λ = a p x m matrix Λ=(λ1',...,λp')';
si = the ith m-dimensional unobservable source vector, si =(si1,...,sim)'; and
εi = the p-dimensional vector of errors or noise terms of the ith observed signal vector εi = (εi1,..., εip)'.
The
observed mixed signal xij is the jth element of the observed mixed signal vector i, which may be thought of as the recorded mixed conversation signal at time increment i, i=1,...,n for microphone j, j=1,...,p. The observed signal xij is a mixture of the components or true unobserved source signal conversations si with error, at time increment i, i=1,...,n. The unobserved source signal sik is the kth component of the unobserved source vector i, which may be thought of as the unobserved source signal conversation of speaker k, k=1,...,m at time increment i, i=1,...,n.
The
model describes the mixing process by writing the observed signal xij as the sum of an overall mean part µj plus a linear combination the unobserved source signal components sik and the observation error εij as

(xij|µj, λj,si,m) = µj + Σk=1m λjk sik + εij
= µj + λj' si + εij.

The
problem at hand is to unmix the unobserved sources. The above has been a very generic description of the BSS problem.



This is an old webpage last updated July 25, 2002 by Daniel Rowe that I reposted on March 24, 2010 after a long hiatus.

Copyright Daniel Rowe
.

Return to Professor Rowe's Webpage